Smearing technique

How to set ISMEAR

For the calculation of the total energy in bulk materials, we recommend the tetrahedron method with Blöchl corrections (ISMEAR=-5). This method also gives a good account of the electronic [[:Category:Density of states|density oIn VASP, it is a good idea to always set a smearing method in the INCAR file because the default choice may lead to incorrect results for some materials. We recommend to default to Gaussian smearing with a relatively small smearing and to set the Fermi energy to the middle of the bandgap

 ISMEAR = 0
 SIGMA = 0.05
 EFERMI = MIDGAP

If you do not know much about your system, we recommend to start with this setup. Below, we explain why this is a good choice and when you should deviate from that. You may also look into K-point integration for the theory behind the methods.

Broadening techniques

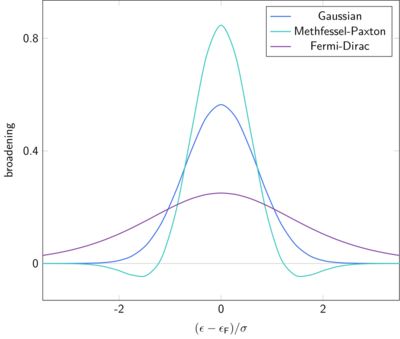
Broading of different smearing techniques near the Fermi energy ϵ_F. The energy is measured in units of the smearing σ (SIGMA). The Methfessel-Paxton method (cyan) is narrower than the Gaussian distribution (blue) but also has negative features. The smearing Fermi-Dirac distribution (purple) corresponds to a temperature but is much broader at the same value of SIGMA

With broadening techniques, each state is occupied not only if the Fermi energy exceeds its eigenvalue but also within a certain width described by SIGMA. Switching from a binary filled/empty to these fractional occupations improves the numeric stability in particular for metallic systems. There is a trade-off in choosing SIGMA: Too large values result in an incorrect total energy while too small smearing ones require a dense mesh of k points.

Gaussian broadening

The Gaussian-smearing method leads to very reasonable results in most cases. Within this method it is necessary to extrapolate from finite SIGMA results to SIGMA = 0 results. You can find an extra line in the OUTCAR file: energy( SIGMA→0 ), giving the extrapolated results. However, this value will not be accurate without systematically reducing SIGMA. Typically, you will need to use a SIGMA of 0.03 to 0.05 for converged results.

Mind: The forces and stress are consistent with the free energy and not with the extrapolated energy SIGMA→0 so make sure that forces and stress are converged with respect to SIGMA as well.

Methfessel-Paxton broadening

The method of Methfessel-Paxton (ISMEAR) results in a very accurate description of the total energy in metals. Nevertheless, the width of the smearing (SIGMA) must be chosen carefully. SIGMA should be as large as possible, while keeping the difference between the free energy and the total energy (i.e. the term entropy T*S) in the OUTCAR file negligible (1 meV/atom). The Methfessel-Paxton method is somewhat easier to use than the Gaussian method since the energies can be corrected for the energy term. Therefore, we recommend to use this method ISMEAR for the calculation of forces and phonon frequencies in metals.

Warning: Avoid using ISMEAR > 0 for semiconductors and insulators, since this often leads to incorrect results. Since the occupancies are not monotonous Methfessel-Paxton does not guarantee deterministic results in systems with a gap. Errors for phonons frequencies can exceed 20%. These errors are very hard to spot if you do not look carefully. For insulators, use Gaussian smearing (ISMEAR = 0) or the tetrahedron method (ISMEAR = -5).

Fermi-Dirac broadening

With the Fermi-Dirac method (ISMEAR = -1), the smearing SIGMA corresponds to the temperature of the electronic system. You should use this method, if this temperature equivalence is important for you, e.g., if you want to compute some properties based on the occupations. In all other cases, you can use the other smearing methods instead.

Tetrahedron methods

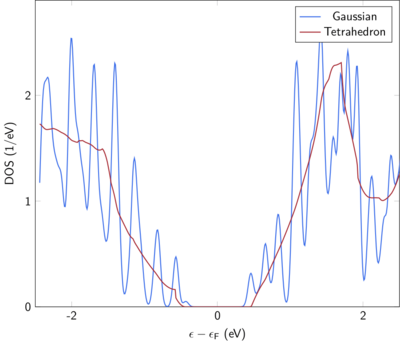
The density of states (DOS) obtained with Gaussian broadening (blue) has much more oscillations than the one obtained with tetrahedron interpolation (red). These spikes correspond to eigenvalue of the bands at different k points. In the tetrahedron method the band is interpolated between the points flattening out the DOS. Another artifact of the broadening is that the DOS extends into the band gap.

In bulk materials, we recommend the tetrahedron method with Blöchl corrections (ISMEAR=-5) for the calculation of very precise total energies or the electronic density of states (DOS). In contrast to broadening methods, the tetrahedron method interpolates between k points of a band. As a consequence, if a band spans a certain energy range, the tetrahedron method will yield no contribution outside of this energy range. Smearing methods will always extend by a width determined by SIGMA beyond this range. You can see in the figure that the resulting onset of band edges is much better captured by the tetrahedron method.

The drawback of the tetrahedron method is that it is not variational with respect to the partial occupancies. Therefore the calculated forces and the stress tensor can be wrong by up to 5 to 10% for metals. Only for semiconductors and insulators, the forces are correct because the partial occupancies do not vary and are either zero or one.

The occupancies in the tetrahedron method are exact for the linear extrapolation of the bands. Partial occupancies arise from the fact that a tetrahedron crosses the Fermi energy. We provide also the option to add temperature on top of the tetrahedron method with ISMEAR = -14 and ISMEAR = -15. This is particularly relevant if accurate occupancies are required e.g. in the context of transport calculations.

Calculation of the Fermi energy

VASP implicitly computes the Fermi energy such that the sum over all occupations results in the number of electrons. In insulators and semiconductors, this choice is not unique if SIGMA is much smaller than the gap. By default EFERMI = LEGACY, VASP will set the Fermi energy typically close to the lower end of the bandgap. This method is not deterministic, i.e., changes to the number of points for the density of states NEDOS can lead to different values. It is also fragile with the Methfessel-Paxton method if you forgot to switch to a different smearing method for a gapped system.

To avoid these issues, we implemented a new method EFERMI = MIDGAP. It will compute the middle of the bandgap and use it as starting point for the interval bisection to compute the Fermi energy. In systems, with a bandgap significantly larger than the smearing width SIGMA the search will terminate immediately. In all other cases, it will fall back to determine the Fermi energy iteratively.

Which method to use

If you have no prior knowledge of your system always use Gaussian smearing ISMEAR = 0 in combination with a small SIGMA = 0.03 to 0.05. This applies in particular if you do not know whether your system is an insulator, a semiconductor or a metal and for high-throughput calculations. This is not the default in VASP, so to be on the safe side, you might want to include this setting in all your INCAR files. You can also switch to set the Fermi energy in the middle of the gap with EFERMI = MIDGAP. Keep in mind to check that your calculations are converged with respect to width SIGMA

For semiconductors or insulators, you can use the tetrahedron method (ISMEAR = -5) if you have at least 4 k points to form a tetrahedron. This eliminates the need to converge the smearing width SIGMA. You need to be sure that the bandgap will not close during the relaxation or molecular dynamics calculation otherwise the forces may be inaccurate.

For relaxations in metals, use ISMEAR=1 or ISMEAR=2 and an appropriate SIGMA value (the entropy term should be less than 1 meV per atom). Often the default value SIGMA = 0.2 is a reasonable choice for metals. Mind again: Avoid using ISMEAR for semiconductors and insulators since it might cause severe problems.

For the calculations of the density of states (DOS) and very accurate total-energy calculations (no relaxation in metals), use the tetrahedron method (ISMEAR = -5). You would often do this at the end of a relaxation for the converged structure with a denser k-point mesh to get an accurate DOS.

Other methods

If you want to keep the occupancies fixed, use ISMEAR = -2. This may be useful to constraint the electronic state. However, keep in mind that this is only an approximation and the real system would relax the occupancies. Please refer to the documentation of FERWE in case you want to set the occupancies manually.

To compare the results of different smearings, you can use ISMEAR = -3. You could use this feature e.g. to converge the SIGMA when Gaussian broadening is used. Please refer to the documentation of SMEARINGS how to set the smearing methods. This feature uses the relaxation engine to change the smearings so you cannot combine it with relaxations.