Constrained–random-phase–approximation formalism

The constrained random-phase approximation (CRPA) is a method that allows to calculate the effective interaction parameter U, J and J' for model Hamiltonians. The main idea is to neglect screening effects of specific target states in the screened Coulomb interaction W of the GW method. The resulting partially screened Coulomb interaction is usually evaluated in a localized basis that spans the target space and is described by the model Hamiltonian. Usually, the target space is low-dimensional (up to 5 states) and therefore allows for the application of a higher level theory, such as dynamical mean field theory (DMFT).

Model Hamiltonians

A model Hamiltonian describes a small subset of electrons around the chemical potential and has, in second quantization, following form

{\displaystyle H = \sum_\sigma \sum_{<ij>} t_{ij}^\sigma c_{i\sigma}^\dagger c_{j\sigma} + \sum_{\sigma\sigma'} \sum_{<ijkl>} U_{ijkl}^{\sigma\sigma'} c_{i\sigma}^\dagger c_{k\sigma'}^\dagger c_{j\sigma} c_{l\sigma'}}

Here, $i,j,k,l$ are site and $\sigma,\sigma'$ spin indices, respectively and the symbol $<\cdots>$ indicates summation over nearest neighbors. The hopping matrix elements $t_{ij}^\sigma$ describe the hopping of electrons (of same spin) between site $i$ and $j$ , while the effective Coulomb matrix elements $U_{ijkl}^{\sigma\sigma'}$ describe the interaction of electrons between sites.

Wannier basis and target space

To use model Hamiltonians successfully a localized basis set is chosen. In most applications this basis set consists of Wannier states that are connected with the Bloch functions $\psi_{n\bf k}^\sigma ({\bf r}) = e^{i{\bf k r}} u_{n\bf k}({r})$ of band $n$ at k-point $k$ with spin $\sigma$ via

{\displaystyle | w_{i\bf R}^\sigma \rangle = \frac{1}{N_k}\sum_{n\bf k} e^{-i {\bf k R}} T_{i n}^{\sigma({\bf k})} | \psi_{n\bf k}^\sigma \rangle }

Usually, the basis set is localized such that the interaction between periodic images can be neglected. This allows to work with the Wannier functions in the unit cell at $\bf R=0$ :

{\displaystyle | w_{i}^\sigma \rangle = \frac{1}{N_k}\sum_{n\bf k} T_{i n}^{\sigma({\bf k})} | \psi_{n\bf k}^\sigma \rangle }

Mind: Here, T instead of the widely used U notation for the transformation matrix is used to avoid confusion with the Hubbard parameter.

In practice one builds a model Hamiltonian only for a small subset of Bloch functions. These target states are typically centered around the chemical potential (or Fermi energy) and are strongly localized around ions. The model Hamiltonian can be solved successfully, only if the target states are well represented by the Wannier basis. As a measure of the Wannier representation one usually compares the original band structure with the Wannier interpolated one.

In the following example (SrVO3) the target space consists of three Bloch bands (red bands) that may be represented well by three Wannier states:

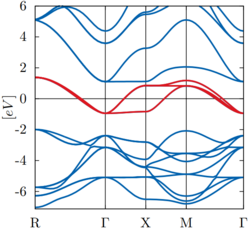
In this optimal case, the Wannier basis contains only target states and no additional Wannier states are required.

More often, however, one has delocalized states that mix with the target space of the model. Without including these crossing states in the Wannier basis, a good representation of the band structure is not possible. Below is an example (face-centered-cubic Ni), where the delocalized s-band (blue) crosses the five target d-states (red):

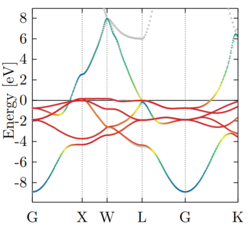
This system requires at least six Wannier states to represent the electronic structure of five target states well. That is, a one-to-one mapping between Bloch and Wannier space requires a six-by-six unitary matrix.

If a modification of the band structure is acceptable within an energy window, these five target states might be disentangled from the remaining ones and one arrives at following picture:

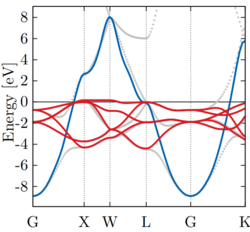
Here the original Bloch bands (gray lines) are projected to five non-crossing Wannier states.

In the following $\cal T$ denotes the subset of Wannier states in the Wannier basis that belong to the target space.

Parameter definitions

Mind: The calculation of the hopping matrix

t

depends on the theory that is used to solve the effective model.

For instance, in DFT+DMFT (often termed LDA+DMFT) one calculates the hopping matrix from Kohn-Sham energies, while in GW+DMFT GW quasi-particle energies are used. If $\epsilon^\sigma_{n\bf k}$ denotes these one-electron energies and $\mu^\sigma$ is the corresponding Fermi energy, the hopping matrix elements are calculated with following formula

{\displaystyle t_{ij}^\sigma = \frac{1}{N_k}\sum_{n\bf k}T_{in}^{*\sigma({\bf k})} (\epsilon^\sigma_{n{\bf k}} - \mu^\sigma) T_{jn}^{\sigma({\bf k})} }

Similarly, Coulomb matrix elements are evaluated from the Bloch representation of the effective Coulomb kernel $U_{{\bf G G}'}({\bf q})$ via

{\displaystyle U_{ijkl}^{\sigma\sigma'} = \frac{1}{N^3_k}\sum_{{\bf k k q}}\sum_{n_1n_2n_3n_4} T_{in_1}^{*({\bf k})} T_{jn_2}^{({\bf k-q})} \langle u_{n_1\bf k}| e^{-i({\bf q + G})\cdot {\bf r}} |u_{n_2\bf k-q}\rangle U_{{\bf G G}'}({\bf q}) \langle u_{n_3\bf k'-q}| e^{i({\bf q - G'})\cdot {\bf r'} }|u_{n_4\bf k'}\rangle T_{kn_3}^{*({\bf k'-q})} T_{ln_4}^{({\bf k'})} }

Mind: The effective Coulomb kernel is frequency dependent and thus the effective interaction in the model as well.

In most applications, however, one considers the static limit $U=U(\omega\to 0)$ .

In practice one often, simplifies the model Hamiltonian further and works with the Hubbard-Kanamori parameters:^[1]

{\displaystyle {\cal U }^{\sigma\sigma'} = \frac 1 N \sum_{i\in \cal T} U_{iiii}^{\sigma\sigma'} }

{\displaystyle {\cal U' }^{\sigma\sigma'} = \frac{1}{N(N-1)}\sum_{i,j \in{\cal T}, i\neq j}^N U_{ijji}^{\sigma\sigma'} }

{\displaystyle {\cal J }^{\sigma\sigma'} = \frac{1}{N(N-1)} \sum_{i,j \in{\cal T}, i\neq j}^N U_{ijij}^{\sigma\sigma'} }

Here $N$ specifies the number of Wannier functions in the target space $\cal T$ .

Effective Coulomb kernel in constrained random-phase approximation

In analogy to the screened Coulomb kernel in GW, the effective coulomb kernel is calculated as

{\displaystyle U^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},\omega)=\left[\delta_{{\bf G}{\bf G}'}-(\chi^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},\omega) - \tilde\chi^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},\omega) ) \cdot V_{{\bf G}{\bf G}'}({\bf q})\right]^{-1}V_{{\bf G}{\bf G}'}({\bf q}) }

In contrast to the GW method, however, the polarizability contains all RPA screening effects, except those from the target space. These effects are described by $\tilde \chi$ and can be separated best in Wannier space. To this end, we work with the target projectors

{\displaystyle P_{mn}^{\sigma({\bf k})} = \sum_{i\in \cal T} T_{i m}^{*\sigma({\bf k})} T_{i n}^{\sigma({\bf k})} }

that filter out target space contributions to each Bloch state. Using these projectors, one can write the Green's functions of the target space

{\displaystyle \tilde G^\sigma({\bf r},{\bf r}',i\tau)=-\frac 1{N_k}\sum_{n{\bf k}} e^{-(\epsilon_{n{\bf k}}-\mu)\tau}\left[\Theta(\tau)(1-f_{n{\bf k}})-\Theta(-\tau)f_{n{\bf k}}\right] \sum_{mm'} P_{n m}^{*\sigma ({\bf k}) } \psi_{m{\bf k}}^{*\sigma }({\bf r}) \psi_{m'{\bf k}}^{\sigma }({\bf r}') P_{m' n}^{\sigma ({\bf k}) } }

an define the screening effects within the target space as follows

{\displaystyle \tilde \chi^{\sigma \sigma'}({\bf r},{\bf r'},i\tau) = -\tilde G^\sigma({\bf r},{\bf r'},i\tau)\tilde G^{\sigma'}({\bf r'},{\bf r},-i\tau) }

After a Fourier transform to reciprocal space and imaginary frequency axis $i\omega$ one ends up with

{\displaystyle \tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)= \frac 1{N_k}\sum_{nn'{\bf k}} f_{n\bf k}(1-f_{n'\bf k-q}) \times \sum_{m_1m_1'm_2m_2' } \int {\rm d}{\bf r }{\rm d}{\bf r'} e^{-i \bf G r} {\rm Re }\left[\frac{ \psi_{m_1 {\bf k }}^{*\sigma }({\bf r }) \psi_{m_1'{\bf k }}^{ \sigma }({\bf r'}) \psi_{m_2 {\bf k-q}}^{*\sigma' }({\bf r'}) \psi_{m_2'{\bf k-q}}^{ \sigma' }({\bf r }) }{ \epsilon_{n{\bf k}} - \epsilon_{n'\bf k-q} - i \omega } \right]e^{-i \bf G' r'} \times P_{m_1 n }^{*\sigma ({\bf k })} P_{m_1' n }^{ \sigma ({\bf k })} P_{m_2 n'}^{*\sigma' ({\bf k-q})} P_{m_2' n'}^{ \sigma' ({\bf k-q})} }

Evaluating the Fourier transform and rearraning one arrives at following expression

{\displaystyle \tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)= \frac 1{N_k}\sum_{nn'{\bf k}} \frac{ f_{n\bf k}-f_{n'\bf k-q} }{ \epsilon_{n{\bf k}} - \epsilon_{n'\bf k-q} - i \omega } \times \sum_{m_1m_2' } P_{m_1 n }^{*\sigma ({\bf k })} \langle u_{m_1 {\bf k }}^{*\sigma } |e^{-i \bf (G+q) r}| u_{m_2'{\bf k-q}}^{ \sigma' } \rangle P_{m_2' n'}^{ \sigma' ({\bf k-q})} \times \sum_{m_1'm_2 } P_{m_2 n'}^{*\sigma' ({\bf k-q})} \langle u_{m_2 {\bf k-q}}^{*\sigma' } |e^{-i \bf (G'-q)r'} | u_{m_1'{\bf k }}^{ \sigma } \rangle P_{m_1' n }^{ \sigma ({\bf k })} }

Note, if the target space forms an isolated set of bands (like in the first example above), the projectors $P$ are identity operators. We call this cRPA approach the projector method.

Mind: The projector method typically yields reasonable Hubbard-Kanamori interactions without additional parameter choices.

In the following two other cRPA methods are discussed.

Disentanglement method

Miyake, Aryasetiawan and Imada^[2] propose to disentangle the target space from the full space, by diagonalizing the Hamiltonian in both spaces independently. This yields a band disentangled band structures similar to the one shown in the third example above. The corresponding target polarizability reduces to a constrained Alder and Wiser expression^[3]^[4]

{\displaystyle \tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)= \frac 1{N_k}\sum_{\bf k}\sum_{nn'\in{\cal T}} \frac{ f_{n\bf k}-f_{n'\bf k-q} }{ \tilde\epsilon_{n{\bf k}} - \tilde\epsilon_{n'\bf k-q} - i \omega } \langle \tilde u_{n {\bf k }}^{*\sigma } |e^{-i \bf (G+q) r}| \tilde u_{n'{\bf k-q}}^{ \sigma' } \rangle \langle \tilde u_{n' {\bf k-q}}^{*\sigma' } |e^{-i \bf (G'-q)r'} | \tilde u_{n{\bf k }}^{ \sigma } \rangle }

,

where $\tilde \epsilon_{n\bf k}^\sigma$ is the disentangled band structure. The resulting Hubbard-Kanamori interactions depend on the chosen energy window of the Wannier functions.

Mind: Typically, this method yields the largest Hubbard-Kanamori interactions.

Weighted CRPA

Sasioglu, Friedrich and Blügel propose an alternative approach,^[5] where the screening effects within the target space are approximated as follows:

{\displaystyle \tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)\approx \frac 1{N_k}\sum_{nn'{\bf k}} \frac{ f_{n\bf k}-f_{n'\bf k-q} }{ \epsilon_{n{\bf k}} - \epsilon_{n'\bf k-q} - i \omega } p_{n\bf k }^{\sigma} p_{n'\bf k-p }^{\sigma'} \langle u_{n {\bf k }}^{*\sigma } |e^{-i \bf (G+q) r}| u_{n'{\bf k-q}}^{ \sigma' } \rangle \langle u_{n' {\bf k-q}}^{*\sigma' } |e^{-i \bf (G'-q)r'} | u_{n'{\bf k }}^{ \sigma } \rangle }

Here the weighting factors

{\displaystyle p_{n\bf k}^\sigma = \sum_{i\in\cal T} |T_{i n}^{\sigma({\bf k})}|^2 , \quad 0 \le p_{n\bf k}^\sigma \le 1 }

measure the probability for $|\psi_{n\bf k}^\sigma\rangle$ being in the target space. This method does not alter the band structure, however, neglects screening effects within the target space.

Mind: Typically, this method yields the smallest Hubbard-Kanamori interactions.

Comparison

The following plot shows calculated Hubbard-Kanamori parameter for the 3d-elements using the three cRPA methods discussed above.

The projector cRPA interactions (red) are in between the interactions of the disentanglement (blue) and weighted (green) method.

References

[vaugier:prb:86-1] L. Vaugier, H. Jiang, and S. Biermann, Phys. Rev. B 86, 165105 (2012).

[miyake:prb:80-2] T. Miyake, F. Aryasetiawan, and M. Imada, Phys. Rev. B 80, 155134 (2009).

[adler:1962-3] S. L. Adler, Phys. Rev. 126, 413 (1962)

[wiser:1963-4] N. Wiser, Phys. Rev. 129, 62 (1963)

[sasioglu:prb:83-5] E. Sasioglu, C. Friedrich, and S. Blügel, Phys. Rev. B 83, 121101 (2011).

[1]

[2]

[3]

[4]

[5]