Nuclephile Substitution CH3Cl - BM
Task
In this example the nucleophile substitution of a Cl- by another Cl- in CH3Cl is simulated using blue-moon sampling.
Input
POSCAR
In the blue-moon sampling method several POSCAR files are used for different values of the collective variable.
BM - POSCAR1 1.0 12.0 0.0 0.0 0.0 12.0 0.0 0.0 0.0 12.0 C H Cl 1 3 2 direct 0.5871322375157908 0.55301018027835513 0.67971406677139101 0.62447012741721697 0.62816585397463176 0.66438574150817353 0.61071464532701736 0.47956072579783432 0.64324619181721654 0.51527571900478364 0.5538828554036046 0.73866022152099475 0.44165342598948132 0.58799096227020642 0.55554878133597507 0.7183326999654791 0.52000018063420794 0.8193619682794645 BM - POSCAR2 1.0 12.0 0.0 0.0 0.0 12.0 0.0 0.0 0.0 12.0 C H Cl 1 3 2 direct 0.5799711358435562 0.55476678237160515 0.67294569944761984 0.62447012741721697 0.62816585397463176 0.66438574150817353 0.61071464532701736 0.47956072579783432 0.64324619181721654 0.51527571900478364 0.5538828554036046 0.73866022152099475 0.44165342598948132 0.58799096227020642 0.55554878133597507 0.72173007151589497 0.51914707229594526 0.82294649849296753 BM - POSCAR3 1.0 12.0 0.0 0.0 0.0 12.0 0.0 0.0 0.0 12.0 C H Cl 1 3 2 direct 0.5728100341713217 0.55652338446485516 0.66617733212384878 0.62447012741721697 0.62816585397463176 0.66438574150817353 0.61071464532701736 0.47956072579783432 0.64324619181721654 0.51527571900478364 0.5538828554036046 0.73866022152099475 0.44165342598948132 0.58799096227020642 0.55554878133597507 0.72512744306631094 0.51829396395768246 0.82653102870647066 BM - POSCAR4 1.0 12.0 0.0 0.0 0.0 12.0 0.0 0.0 0.0 12.0 C H Cl 1 3 2 direct 0.59507047500290222 0.57244270557313315 0.66746206851391643 0.54049944202575662 0.60714565557876798 0.72974089156310651 0.66455173208019991 0.53195474180779956 0.70393149950062939 0.55747027889637368 0.53034945501598485 0.59848340437508063 0.65618532162250798 0.69708568471255838 0.57638613391759708 0.5000409863126819 0.4022456289304116 0.80922741395305486 BM - POSCAR5 1.0 12.0 0.0 0.0 0.0 12.0 0.0 0.0 0.0 12.0 C H Cl 1 3 2 direct 0.59887853190304419 0.57974515358235179 0.6617842250921081 0.54049944202575662 0.60714565557876798 0.72974089156310651 0.66455173208019991 0.53195474180779956 0.70393149950062939 0.55747027889637368 0.53034945501598485 0.59848340437508063 0.65618532162250798 0.69708568471255838 0.57638613391759708 0.4980707241384853 0.3987068989373313 0.8121665955404771 BM - POSCAR6 1.0 12.0 0.0 0.0 0.0 12.0 0.0 0.0 0.0 12.0 C H Cl 1 3 2 direct 0.60268658880318615 0.58704760159157043 0.65610638167029967 0.54049944202575662 0.60714565557876798 0.72974089156310651 0.66455173208019991 0.53195474180779956 0.70393149950062939 0.55747027889637368 0.53034945501598485 0.59848340437508063 0.65618532162250798 0.69708568471255838 0.57638613391759708 0.4961004619642887 0.395168168944251 0.81510577712789944 BM - POSCAR7 1.0 12.0 0.0 0.0 0.0 12.0 0.0 0.0 0.0 12.0 C H Cl 1 3 2 direct 0.60649464570332823 0.59435004960078897 0.65042853824849134 0.54049944202575662 0.60714565557876798 0.72974089156310651 0.66455173208019991 0.53195474180779956 0.70393149950062939 0.55747027889637368 0.53034945501598485 0.59848340437508063 0.65618532162250798 0.69708568471255838 0.57638613391759708 0.4941301997900921 0.39162943895117058 0.81804495871532179
KPOINTS
Automatic 0 Gamma 1 1 1 0. 0. 0.
- For isolated atoms and molecules interactions between periodic images are negligible (in sufficiently large cells) hence no Brillouin zone sampling is necessary.
INCAR
PREC=Low EDIFF=1e-6 LWAVE=.FALSE. LCHARG=.FALSE. NELECT=22 NELMIN=4 LREAL=.FALSE. ALGO=VeryFast ISMEAR=-1 SIGMA=0.0516 ############################# MD setting ################################## IBRION=0 # MD simulation NSW=1000 # number of steps POTIM=1 # integration step TEBEG=600 # simulation temperature MDALGO=11 # Andersen thermostat ANDERSEN_PROB=0.10 # collision probability LBLUEOUT=.TRUE. # write down output needed to # compute free-energy gradient ##############################################################################
- The setting LBLUEOUT=.TRUE. tells VASP to write out the information needed for the computation of free energies.
Calculation
In the blue-moon sampling, the free energy difference is computed by integration of the free energy gradients computed for several points differing in the value of the collective variable distributed between known inital and final states. The gradients for each point are computed within a constrained molecular dynamics simulation (note the value of STATUS=0 for the collective variable defined in the ICONST file).
Running the calculation
The mass for hydrogen in this example is set 3.016 a.u. corresponding to the tritium isotope. This way larger timesteps can be chosen for the MD (note that the free energy is independent of the masses of atoms). The simulation for each of the points along the reaction coordinate is performed in a separate directory called 1, 2, ..., 7. These are created automatically by the run script. For practical reasons, we split our (presumably long) blue-moon calculation into shorter runs of length of 1000 fs (NSW=1000; POTIM=1). This is done automatically in the script run which looks as follows:
#!/bin/bash
drct=$(pwd)
runvasp="mpirun -np x executable_path"
# ensure that this sequence of MD runs is reproducible - not needed
# in a real-world application
rseed="RANDOM_SEED = 311137787 0 0"
#c loop over "points" (i.e. structures
#c with difference value of CV)
for j in 1 2 3 4 5 6 7
do
cd $drct
mkdir ${j}
cp POSCAR.$j ${j}/POSCAR
cp POTCAR KPOINTS ICONST $j
cd $j
#c here we perform sequence of MD runs
#c for each point
step=1
while [ $step -le 7 ]
do
if ! test -f report.${step}
then
# ensure that this sequence of MD runs is reproducible
cp ${drct}/INCAR .
echo $rseed >> INCAR
cp POSCAR POSCAR.$step
$runvasp
# ensure that this sequence of MD runs is reproducible
rseed=$(grep RANDOM_SEED REPORT |tail -1)
#c backup some important files
cp CONTCAR POSCAR
cp REPORT report.$step
grep F OSZICAR > osz.$step
cp vasprun.xml vasprun.xml.$step
fi
let step=step+1
done
done
Free-energy profile
The free energy gradient is obtained as a ratio of two averages (see Constrained molecular dynamics). This is done by the script fgradBM.sh, which writes the free energy gradient vs. the collective variable to the file grad.dat:
#!/bin/bash
#c equilibration period
equil=2000
if [ -f "grad.dat" ]; then
rm grad.dat
fi
touch grad.dat
for i in 1 2 3 4 5 6 7
do
rm rep.*
j=1
while [ $j -le 100 ]
do
if test -f $i/report.$j
then
grep b_m $i/report.$j >> rep.$i.1
fi
let j=j+1
done
#c obtain ingredients for FE-gradfient calculation
#c (cf. eq. 12 in JPCM 20, 064211 (2008))
if test -f $i/report.1
then
#c value of the constrained coordinate
x1=$(grep cc $i/report.1|head -1|awk '{print $3}')
nlines=$(wc -l rep.$i.1|awk '{print $1}')
let prod=nlines-equil
#c calculation of the FE-gradfient
#c (cf. eq. 12 in JPCM 20, 064211 (2008))
zet=$(grep b_m rep.$i.1|tail -$prod |awk 'BEGIN {a=0.} {a+=$3} END {print a/NR}')
g1=$(grep b_m rep.$i.1|tail -$prod |awk 'BEGIN {a=0.} {a+=$5} END {print a/NR/"'${zet}'"}')
echo $x1 $g1 >> grad.dat
fi
done
To execute that script type:
bash ./fgradBM.sh
For our purposes, a simple trapezoidal rule can be used for the integration of gradients. For accurate calculations, more sohpisticated integration schemes should be considered. The free energy vs. collective variable is obtained by forward integration using the script integrateForward.py:
#!/usr/bin/python
import string
import sys
f=sys.argv[1]
f=open(f,'r')
r=[]
g=[]
for line in f.readlines():
line=string.split(line)
num=len(line)
if len(line)==2:
r.append(float(line[0]))
g.append(float(line[1]))
f.close()
tg=0.0
print r[0],tg
for i in range(1,len(r)):
gg=0.5*(r[i]-r[i-1])*(g[i]+g[i-1])
tg+=gg
print r[i],tg
To execute that script type and write to the file free_energy.dat:
python integrateForward.py grad.dat > free_energy.dat
Finally to plot that file type:
gnuplot -e "set terminal jpeg; set xlabel 'Collective variable (Ang)'; set ylabel 'Free energy (eV)'; set style data lines; plot 'free_energy.dat'" > free_energy.jpg
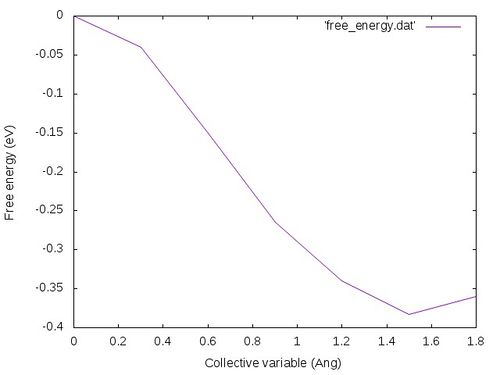
The free energy profile should look like the following:
Note that much longer simulations should be performed (typically a few tens or hundreds of ps) in order to achieve well converged averages needed in accurate calculations.