|
|
| Line 79: |
Line 79: |
|
| |
|
| :<math> | | :<math> |
| \mathtt{ENMAX}=\frac{\hbar^2}{2m}\left( G_{\rm ini} + |q| \right)^2 | | \mathtt{ENMAX} \geq \frac{\hbar^2}{2m}\left( G_{\rm ini} + |q| \right)^2 |
| </math> | | </math> |
|
| |
|
Revision as of 13:52, 6 July 2018
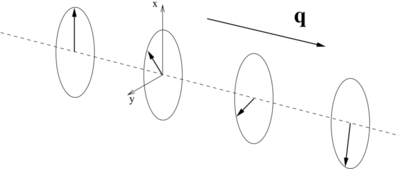
Generalized Bloch condition
Spin spirals may be conveniently modeled using a generalization of the Bloch condition (set LNONCOLLINEAR=.TRUE. and LSPIRAL=.TRUE.):
![{\displaystyle
\left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r) \\
\Psi^{\downarrow}_{\bf k}(\bf r) \end{array} \right] = \left(
\begin{array}{cc}
e^{-i\bf q \cdot \bf R / 2} & 0\\
0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[
\begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\
\Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right],
}](/wiki/index.php?title=Special:MathShowImage&hash=d87ea979867db8fcc85d3f002be8e039&mode=mathml)
i.e., from one unit cell to the next the up- and down-spinors pick up an additional phase factor of  and
and  , respectively,
where R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector.
, respectively,
where R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector.
The spin-spiral propagation vector is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice, and has to be specified by means of the QSPIRAL-tag.
The generalized Bloch condition above gives rise to the following behavior of the magnetization density:

This is schematically depicted in the figure at the top of this page:
the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.
Basis set considerations
The generalized Bloch condition redefines the Bloch functions as follows:


This changes the Hamiltonian only minimally:

where in  and
and  the kinetic energy of a plane wave component changes to:
the kinetic energy of a plane wave component changes to:


In the case of spin-spiral calculations the cutoff energy of the basis set of the individual spinor components is specified by means of the ENINI-tag.
Additionally one needs to set ENMAX appropriately:
ENMAX needs to be chosen larger than ENINI, and large enough so that the plane wave components of both the up-spinors as well as the components of the down-spinor all have a kinetic energy smaller than ENMAX.
This is the case when:

where

In most cases it is more than sufficient to set ENMAX=ENINI+100.

