Spin spirals

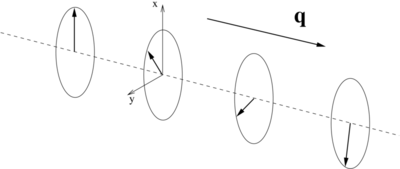
Generalized Bloch condition

Spin spirals may be conveniently modeled using a generalization of the Bloch condition (set LNONCOLLINEAR=.TRUE. and LSPIRAL=.TRUE.):

$\left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r) \\ \Psi^{\downarrow}_{\bf k}(\bf r) \end{array} \right] = \left( \begin{array}{cc} e^{-i\bf q \cdot \bf R / 2} & 0\\ 0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ \Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right],$

i.e., from one unit cell to the next the up- and down-spinors pick up an additional phase factor of $\exp(-i{\bf q}\cdot {\bf R}/2)$ and $\exp(+i{\bf q}\cdot {\bf R}/2)$, respectively, where R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector.

The spin-spiral propagation vector is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice, and has to be specified by means of the QSPIRAL-tag.

The generalized Bloch condition above gives rise to the following behavior of the magnetization density:

${\bf m} ({\bf r} + {\bf R})= \left( \begin{array}{c} m_x({\bf r}) \cos({\bf q} \cdot {\bf R}) - m_y({\bf r}) \sin({\bf q} \cdot {\bf R}) \\ m_x({\bf r}) \sin({\bf q} \cdot {\bf R}) + m_y({\bf r}) \cos({\bf q} \cdot {\bf R}) \\ m_z({\bf r}) \end{array} \right)$

This is schematically depicted in the figure at the top of this page: the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.

Basis set considerations

The generalized Bloch condition redefines the Bloch functions as follows:

$\Psi^{\uparrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\uparrow}_{\bf k \bf G} e^{i(\bf k + \bf G -\frac{\bf q}{2})\cdot \bf r}$

$\Psi^{\downarrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\downarrow}_{\bf k \bf G} e^{i(\bf k + \bf G +\frac{\bf q}{2})\cdot \bf r}$

This changes the Hamiltonian only minimally:

$\left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} \\ V^{\downarrow\uparrow}_{\rm xc} & H^{\downarrow\downarrow} \end{array}\right) \rightarrow \left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} e^{-i\bf q \cdot \bf r} \\ V^{\downarrow\uparrow}_{\rm xc}e^{+i\bf q \cdot \bf r} & H^{\downarrow\downarrow} \end{array}\right),$

where in $H^{\uparrow\uparrow}$ and $H^{\downarrow\downarrow}$ the kinetic energy of a plane wave component changes to:

$H^{\uparrow\uparrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} - {\bf q} /2|^2$

$H^{\downarrow\downarrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} + {\bf q} /2|^2$