Spin spirals: Difference between revisions
Vaspmaster (talk | contribs) No edit summary |
Vaspmaster (talk | contribs) No edit summary |
||
| Line 16: | Line 16: | ||
</span> | </span> | ||
''i.e.'', from one unit cell to the next the up- and down-spinors pick up an additional phase factor of <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math> and <math>\exp(+i{\bf q}\cdot {\bf R}/2)</math>, respectively | ''i.e.'', from one unit cell to the next the up- and down-spinors pick up an additional phase factor of <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math> and <math>\exp(+i{\bf q}\cdot {\bf R}/2)</math>, respectively, | ||
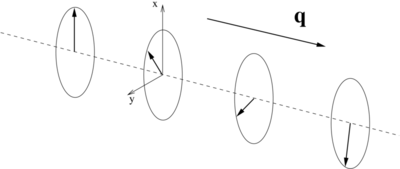
where, '''R''' is a lattice vector of the crystalline lattice, and '''q''' is the so-called spin-spiral propagation vector. | |||
The | |||
The spin-spiral propagation vector is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice, and has to be specified by means of the {{TAG|QSPIRAL}}-tag. | |||
This generalized Bloch condition gives rise to the following behavior of the magnetization density: | This generalized Bloch condition gives rise to the following behavior of the magnetization density: | ||
Revision as of 12:53, 6 July 2018
Generalized Bloch condition
Spin spirals may be conveniently modeled using a generalization of the Bloch condition:
i.e., from one unit cell to the next the up- and down-spinors pick up an additional phase factor of and , respectively, where, R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector.
The spin-spiral propagation vector is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice, and has to be specified by means of the QSPIRAL-tag.
This generalized Bloch condition gives rise to the following behavior of the magnetization density:
This is schematically depicted in the figure at the top of this page: the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.