Supercell core-hole theory

In the Super-cell core-hole method (SCH) a chosen core electron is removed from the core leaving behind a positive charge. Since one wants to simulate the excitation of this electron into energetically higher lying states, one electron is added to valence/conduction bands resembling the final state of the excitation process (this is also referred to as the final state approximation). With this setup a fully self-consistent electronic minimization is carried out. The core hole is perfectly screened by the other electrons in metals so there should be no difference between core-hole calculations and regular calculations. In semiconductors and insulators, this screening is very weak and a very strong attraction between the electrons and hole occurs, which results in not only a lowering of the excited states compared to the valence states, but also a very strong change of the valence/conduction band structure. Hence the relaxation of the valence/conduction electrons is the main effect in core-hole calculations. Fortunately the relaxation of the core states in core-hole calculations is negligible. This makes the implementation into a PAW framework smooth, since no on-the fly recalculation of PAW potentials is needed in every step of the electronic self-consistent cycle.

Very important is that a sufficiently large super cell is used to minimize the interaction of neighboring core holes within periodic boundary conditions. Hence the computational expense within this methods comes mainly from the use of large super cells. Nevertheless this method is usually still computationally cheaper than the BSE method for core electrons.

Excited electron treatment

Schematic representation of the self-interaction effects in the XCH spectra.

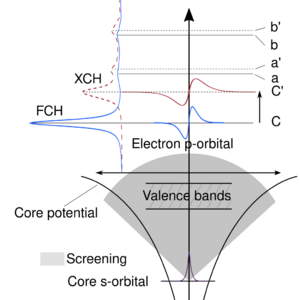
Two different approaches can be used to treat the excited electron in SCH. The excited electron can be placed into the lowest conduction band in the excited electron and core-hole (XCH) approach, alternatively the excited electron can be accounted for by a negative background charge to ensure that the cell remains neutral in the full core-hole (FCH) method. These two approaches are discussed and compared in great detail in Ref. . The main shortcoming of the XCH approach comes from the self-interaction effects of the electron exchange and correlation functional caused when the excited electron is placed in the conduction band, which is more pronounced for strongly localized conduction bands. The effects of the self-interaction error are schematically depicted in the figure on the right. The figure sketches a s to p transition in the K-edge. The lowest conduction band at level C is represented by a p orbital. The self-interaction error in turn causes two effects: First, it shifts up the energy level of the occupied conduction band from the initial energy C to the new energy C'. Second, it delocalizes the orbital. In FCH, by placing the negative charge in the background we avoid such self-interaction effects. For systems, where the conduction bands are weakly localized, both approaches produce very similar results. However, for systems with localized conduction states, e.g. Li-halides, the FCH has been shown to yield better agreement with the results of the BSE+GW calculations as well as experimental spectra .

Dielectric function used in the SCH method

Since the wave length of the electromagnetic waves in absorption spectroscopy is usually much larger than the characteristic momentum in solids, we start from the transversal expression for the imaginary part of the dielectric function in the long wavelength limit ($\mathbf{q}=0$) which is directly proportional to the absorption spectrum

$\epsilon_{\alpha \beta}^{(2)} (\omega,\mathbf{q}=0) = \frac{4 \pi^{2} e^{2} \hbar^{4}}{\Omega \omega^{2} m_{e}^{2}} \sum\limits_{c,v,\mathbf{k}} 2w_{\mathbf{k}} \delta(\varepsilon_{c\mathbf{k}}-\varepsilon_{v\mathbf{k}}-\omega) \times M_{\alpha}^{v\rightarrow c} {M_{\beta}^{v\rightarrow c}}^{*}$

where $M$ and $\varepsilon$ denote momentum matrix elements and orbital energies. Here we consider excitations only between valence ($v$) and conduction ($c$) bands. The components of the dielectric tensor are indexed by the Cartesian indices $\alpha$ and $\beta$. $\Omega$, $e$ and $m_{e}$ denote the unit cell volume, electron charge and mass of the electron, respectively. In the PAW method the all-electron orbitals $|\psi_{n\bold{k}}\rangle$ are given by a linear transformation of the pseudo orbitals $|\tilde{\psi}_{n\bold{k}}\rangle$:

$|\psi_{n\bold{k}}\rangle = |\tilde{\psi}_{n\bold{k}}\rangle + \sum\limits_{i} (|\phi_{i}\rangle - |\tilde{\phi}_{i}\rangle) \langle \tilde{p}_{i} |\tilde{\psi}_{n\bold{k}}\rangle.$

The pseudo orbitals depend on the band index $n$ and crystal momentum $\bold{k}$. $|\phi_{i}\rangle$, $|\tilde{\phi}_{i}\rangle$ and $|\tilde{p}_{i}\rangle$ are all-electron partial waves, pseudo partial waves and the projectors, respectively. The index $i$ is a shorthand for the atomic site and other indices enumerating these quantities at each site (such as angular and magnetic quantum numbers). In the PAW formalism, the matrix elements are given by

$M_{\alpha}^{v\rightarrow c} = \langle \psi_{c \mathbf{k}} |i \nabla_{\alpha} - \mathbf{k}_{\alpha}| \psi_{v\mathbf{k}} \rangle = \langle \tilde{\psi}_{c\mathbf{k}}| i \nabla_{\alpha}-\mathbf{k}_{\alpha}|\tilde{\psi}_{v\mathbf{k}} \rangle + \sum\limits_{ij} \langle \tilde{\psi}_{c\mathbf{k}} | \tilde{p}_{i} \rangle \langle \tilde{p}_{j} | \tilde{\psi}_{v\mathbf{k}} \rangle i \left(\langle \phi_{i}| \nabla_{\alpha}| \phi_{j} \rangle - \langle \tilde{\phi}_{i}| \nabla_{\alpha}| \tilde{\phi}_{j} \rangle \right).$

where the one-center terms are calculated within the PAW sphere for each atom.

Since in X-ray absorption spectroscopy, one only considers one core hole at a single site, we can from now on restrict the equations to a single site. The index $i$ then only enumerates the main quantum number, the angular and the magnetic quantum numbers. As usual in the PAW method, using the completeness relation, $\sum_{i} |\tilde{p}_{i}\rangle \langle \tilde{\phi}_{i}| = 1$, the first and third term in the previous equation cancel each other leading to the following simplified matrix elements $M^{\mathrm{core}\rightarrow c\mathbf{k}}_{\alpha}=\sum\limits_{i}\langle \tilde{\psi}_{c\mathbf{k}} | \tilde{p}_{i} \rangle \langle\phi_{i}| \nabla_{\alpha}| \phi_{\mathrm{core}}\rangle.$

Also the summation over bands can be limited to the conduction bands $c$

$\epsilon_{\alpha \beta}^{(2)} (\omega) = \frac{4 \pi^{2} e^{2} \hbar^{4}}{\Omega \omega^{2} m_{e}^{2}} \sum\limits_{c,\mathbf{k}} 2w_{\mathbf{k}}\delta(\varepsilon_{c\mathbf{k}}-\varepsilon_{\mathrm{core}}-\omega) \times M^{\mathrm{core}\rightarrow c\mathbf{k}}_\alpha {M^{\mathrm{core}\rightarrow c\mathbf{k}}_\beta}^*.$

---