LSINGLES: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{TAGDEF|LSINGLES|.TRUE. {{!}} .FALSE.|.FALSE.}} | {{TAGDEF|LSINGLES|.TRUE. {{!}} .FALSE.|.FALSE.}} | ||
Description: Switch on singles contribution to correlation energy for | Description: Switch on singles contribution to correlation energy for [[Practical_guide_to_GW_calculations#Low_scaling_GW_algorithms|GW algorithms]].{{cite|klimes:jcp:143}} | ||
---- | ---- | ||
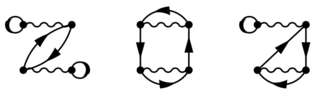
{{TAG|LSINGLES}} enables the calculation of the singles contributions to the correlation energy that can be represented by the following Feynman (time-ordered) diagrams:{{cite|kaltak:thesis2015}}{{cite|klimes:jcp:143}} | {{TAG|LSINGLES}} enables the calculation of the singles contributions to the correlation energy that can be represented by the following Feynman (time-ordered) diagrams:{{cite|kaltak:thesis2015}}{{cite|klimes:jcp:143}} | ||
Revision as of 10:35, 20 October 2023
LSINGLES = .TRUE. | .FALSE.
Default: LSINGLES = .FALSE.
Description: Switch on singles contribution to correlation energy for GW algorithms.[1]
LSINGLES enables the calculation of the singles contributions to the correlation energy that can be represented by the following Feynman (time-ordered) diagrams:[2][1]
LSINGLES is used in combination with the low-scaling ACFDT/RPA and GW algorithms.
If the ACFDT/RPA algorithm is selected with ALGO=RPAR|ACFDTR and LSINGLES is set, the code calculates two singles contributions and writes following lines to OUTCAR
HF single shot energy change -1.23182672 renormalized HF singles -1.23310555
Here, renomalized HF singles corresponds to the renormalized singles contribution suggested by Ren and coworkers:[3]
This contribution accounts for the change of the mean-field exchange energy and can be derived consistently within the AC-FDT framework as described in Sec. II D Eq. (28) of Klimeš et al.[1]
In contrast, the HF single shot energy change line contains the somewhat simpler contribution[1]
where is the Hartree-Fock density matrix, determined for the Hartree-Fock Hamiltonian and is the Kohn-Sham density matrix. In all practical calculations, we found that both values, the single-shot HF and renormalized singles contributions, are exceedingly close to each other.
If the GW algorithm is selected with ALGO=G0W0R, the OUTCAR contains also the singles contribution beyond the Hartree-Fock level
where is the RPA density matrix.[1] For versions <= 6.4.2, this contribution is not directly printed to file. However, the first and second term is printed to OUTCAR:
Energies using frozen KS orbitals
Hartree-Fock free energy of the ion-electron system (eV)
...
eigenvalues EBANDS = -88.61789695 <--------Tr{ gam_DFT h_HF}---------
...
Energies after update of density matrix
Hartree-Fock free energy of the ion-electron system (eV)
...
eigenvalues EBANDS = -89.68870320 <--------Tr{ gam_RPA h_HF}---------
...
Version >6.4.2 writes the GWSE singles contribution to OUTCAR:
GWSE singles contribution: -1.07080625
| Mind: The singles contribution is calculated correctly only for the default NATURALO=2. |
The ACFDT total energy in the limit of infinite energy cutoff is then obtained by adding the singles contribution to the value of
HF+E_corr(extrapolated) = -153.98810072 eV
Related tags and articles
- NATURALO natural orbital selection for RPA and GW calculations
- ALGO for response functions and RPA calculations
- for an overview on total energies using the ACFDT/RPA formalism
- for a practical guide to GW calculations
- Basis set convergence of ACFDT/RPA calculations