Constructing Wannier orbitals: Difference between revisions
(→SCDM and Wannier90: Make more general) |
(Change INCAR blocks to use TAGBL) |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 30: | Line 30: | ||
In general, <math>A_{mn \mathbf{k}}</math> is not going to be a unitary matrix. | In general, <math>A_{mn \mathbf{k}}</math> is not going to be a unitary matrix. | ||
It could in principle be used to transform the Bloch orbitals into a set of non-orthogonal Wannier orbitals. | It could, in principle, be used to transform the Bloch orbitals into a set of non-orthogonal Wannier orbitals. | ||
However, for many applications it is desirable to have orthonormal Wannier orbitals, such as for Wannier interpolation. | However, for many applications, it is desirable to have orthonormal Wannier orbitals, such as for Wannier interpolation. | ||
Therefore, <math>A_{mn \mathbf{k}}</math> needs to | Therefore, <math>A_{mn \mathbf{k}}</math> needs first to be orthonormalized. | ||
In VASP, we employ a one-shot orthonormalization procedure that uses the [https://en.wikipedia.org/wiki/Singular_value_decomposition singular-value decomposition] (SVD) of <math>A_{mn \mathbf{k}}</math>: | In VASP, we employ a one-shot orthonormalization procedure that uses the [https://en.wikipedia.org/wiki/Singular_value_decomposition singular-value decomposition] (SVD) of <math>A_{mn \mathbf{k}}</math>: | ||
| Line 42: | Line 42: | ||
U_{mn\mathbf{k}} = [DV^\dagger]_{mn\mathbf{k}}. | U_{mn\mathbf{k}} = [DV^\dagger]_{mn\mathbf{k}}. | ||
</math> | </math> | ||
In contrast to iterative methods (e.g., Gram-Schmidt orthogonalization), the SVD orthogonalization operates simultaneously on all local functions. | |||
This ensures that the symmetry properties of the local functions encoded in <math>A_{mn \mathbf{k}}</math> are preserved during the orthonormalization procedure. | This ensures that the symmetry properties of the local functions encoded in <math>A_{mn \mathbf{k}}</math> are preserved during the orthonormalization procedure. | ||
| Line 55: | Line 55: | ||
To find a good representation of the electronic band structure in terms of Wannier orbitals, it is important to choose suitable projection targets. | To find a good representation of the electronic band structure in terms of Wannier orbitals, it is important to choose suitable projection targets. | ||
In general, this can be a difficult task as some bands hybridize and disperse, changing electronic character as a function of the Bloch vector <math>\mathbf{k}</math>. | In general, this can be a difficult task as some bands hybridize and disperse, changing electronic character as a function of the Bloch vector <math>\mathbf{k}</math>. | ||
It is thus expedient to | It is thus expedient to understand the relevant electronic bands before attempting a Wannierization using {{TAG|LOCPROJ}}. | ||
To gain insight into the electronic character of certain bands, you can use the {{TAG|LORBIT}} tag. | To gain insight into the electronic character of certain bands, you can use the {{TAG|LORBIT}} tag. | ||
| Line 71: | Line 71: | ||
This decomposes the bands into <math>l</math> and <math>m</math> quantum numbers in terms of spherical harmonics. | This decomposes the bands into <math>l</math> and <math>m</math> quantum numbers in terms of spherical harmonics. | ||
We get information on each k-point in the [[PROCAR]] file. | We get information on each k-point in the [[PROCAR]] file. | ||
Here is the start of the file which contains information about the Γ-point: | Here is the start of the file, which contains information about the Γ-point: | ||
<pre> | <pre> | ||
PROCAR lm decomposed | PROCAR lm decomposed | ||
| Line 112: | Line 112: | ||
We seek to map the four bands in the simulation to four Wannier orbitals, so we choose to setup four sp-3 hybrids on one atom. | We seek to map the four bands in the simulation to four Wannier orbitals, so we choose to setup four sp-3 hybrids on one atom. | ||
The minimal INCAR file used in this example looks like this: | The minimal INCAR file used in this example looks like this: | ||
{{TAGBL|ISMEAR}} = 0 ! use Gaussian smearing for insulator | |||
{{TAGBL|SIGMA}} = 0.01 ! use small smearing | |||
{{TAGBL|NBANDS}} = 4 ! use only 4 bands | |||
{{TAGBL|LOCPROJ}} = 1 : sp3 : Hy 1 4. ! ... to map onto 4 sp-3 functions | |||
The last part of the {{TAG|LOCPROJ}} setting (<tt>Hy 1 4.</tt>) specifies that we want Hyrdogen-like atomic orbitals (spherical harmonics) with main quantum number <math>n = 1</math> and a diffusivity of <math>\alpha = 4</math>. | The last part of the {{TAG|LOCPROJ}} setting (<tt>Hy 1 4.</tt>) specifies that we want Hyrdogen-like atomic orbitals (spherical harmonics) with main quantum number <math>n = 1</math> and a diffusivity of <math>\alpha = 4</math>. | ||
The diffusivity influences the spread of the local function. | The diffusivity influences the spread of the local function. | ||
A higher value generally results in a higher degree of localization. | A higher value generally results in a higher degree of localization. | ||
This is beneficial for Wannier interpolation and yields Wannier orbitals of higher quality in that regard. | This is beneficial for Wannier interpolation and yields Wannier orbitals of higher quality in that regard. | ||
{{NB | {{NB|tip|You may also choose to use the PAW information to specify local orbitals with {{TAG|LOCPROJ}}. In this case, you should use {{TAGO|LORBIT|11}} to extract the relevant information from the basis.}} | ||
For this example calculation, we use a relatively course Γ-centered regular mesh of <tt>4x4x4</tt> k-points. | For this example calculation, we use a relatively course Γ-centered regular mesh of <tt>4x4x4</tt> k-points. | ||
| Line 157: | Line 157: | ||
Once again, we choose {{TAGO|NBANDS|4}} and we set {{TAGO|NUM_WANN|4}} as well. | Once again, we choose {{TAGO|NBANDS|4}} and we set {{TAGO|NUM_WANN|4}} as well. | ||
The minimal [[INCAR]] file for this example looks like this: | The minimal [[INCAR]] file for this example looks like this: | ||
{{TAGBL|ISMEAR}} = 0 ! use Gaussian smearing for insulator | |||
{{TAGBL|SIGMA}} = 0.01 ! use small smearing | |||
{{TAGBL|NBANDS}} = 4 ! use only 4 bands | |||
{{TAGBL|NUM_WANN}} = 4 ! ... to map onto 4 Wannier orbitals | |||
{{TAGBL|LSCDM}} = true ! ... using the SCDM method | |||
For this example calculation, we use the same course Γ-centered regular mesh of <tt>4x4x4</tt> k-points as before. | For this example calculation, we use the same course Γ-centered regular mesh of <tt>4x4x4</tt> k-points as before. | ||
We also specify the same k-point path for [[KPOINTS_OPT]] and [[KPOINTS_WAN]] to perform band-structure calculations. | We also specify the same k-point path for [[KPOINTS_OPT]] and [[KPOINTS_WAN]] to perform band-structure calculations. | ||
| Line 216: | Line 216: | ||
The minimal [[INCAR]] file for this example is provided below: | The minimal [[INCAR]] file for this example is provided below: | ||
{{TAGBL|ISMEAR}} = 0 ! use Gaussian smearing for insulator | |||
{{TAGBL|SIGMA}} = 0.01 ! use small smearing | |||
{{TAGBL|NBANDS}} = 16 ! use 16 bands, including unoccupied states | |||
{{TAGBL|NUM_WANN}} = 9 ! ... to map to 9 Wannier orbitals | |||
{{TAGBL|LSCDM}} = true ! ... using the SCDM method | |||
{{TAGBL|CUTOFF_TYPE}} = erfc ! choose erfc cutoff function | |||
{{TAGBL|CUTOFF_MU}} = 10 ! ... and place it at 10 eV | |||
{{TAGBL|CUTOFF_SIGMA}} = 0.1 ! ... with a width of 0.1 eV | |||
The initial k-point mesh is chosen to be <tt>8x8x8</tt> Γ-centered. | The initial k-point mesh is chosen to be <tt>8x8x8</tt> Γ-centered. | ||
| Line 245: | Line 245: | ||
To generate MLWFs from VASP orbitals, you can add the following lines to your [[INCAR]] file: | To generate MLWFs from VASP orbitals, you can add the following lines to your [[INCAR]] file: | ||
{{TAGBL|LWANNIER90}} = true # or lwannier90_run = true | |||
{{TAGBL|WANNIER90_WIN}} = " | |||
dis_num_iter = 100 | |||
num_iter = 100 | |||
" | " | ||
where <tt>dis_num_iter</tt> specifies the number of iteration during Wannier90's disentanglement procedure and <tt>num_iter</tt> the number of iteration during the MLWF procedure. | where <tt>dis_num_iter</tt> specifies the number of iteration during Wannier90's disentanglement procedure and <tt>num_iter</tt> the number of iteration during the MLWF procedure. | ||
{{NB|important|Make sure that VASP is compiled with the [[Precompiler options#-DVASP2WANNIER90|VASP2WANNIER90]] precompiler option.}} | {{NB|important|Make sure that VASP is compiled with the [[Precompiler options#-DVASP2WANNIER90|VASP2WANNIER90]] precompiler option.}} | ||
| Line 264: | Line 264: | ||
Afterwards, run Wannier90 to generate MLWFs (all of this can be done in one run when setting {{TAGO|LWANNIER90_RUN|true}}). | Afterwards, run Wannier90 to generate MLWFs (all of this can be done in one run when setting {{TAGO|LWANNIER90_RUN|true}}). | ||
At this point, you can use the functionality available in Wannier90 to plot the band structure, the orbitals, etc. | At this point, you can use the functionality available in Wannier90 to plot the band structure, the orbitals, etc. | ||
When plotting orbitals using Wannier90, in addition to {{TAGO|LWRITE_MMN_AMN|true}}, it may also be necessary to set {{TAGO|LWRITE_UNK|true}}. | When plotting orbitals using Wannier90, in addition to {{TAGO|LWRITE_MMN_AMN|true}}, it may also be necessary to set {{TAGO|LWRITE_UNK|true}}. | ||
| Line 271: | Line 270: | ||
== Related tags and articles== | == Related tags and articles== | ||
{{TAG|LSCDM}}, | {{TAG|LSCDM}}, | ||
{{TAG|LOCPROJ}}, | |||
{{TAG|CUTOFF_TYPE}}, | {{TAG|CUTOFF_TYPE}}, | ||
{{TAG|CUTOFF_MU}}, | {{TAG|CUTOFF_MU}}, | ||
| Line 277: | Line 277: | ||
== References == | == References == | ||
<references/> | <references/> | ||
[[Category:Wannier functions]][[Category:Howto]] | |||
Latest revision as of 09:07, 18 June 2024
Wannier orbitals are an important tool to study chemical bonding. They also form the basis of various interpolation techniques. As a quick summary, a Wannier orbital is a function obtained from a linear combination of the Bloch (Kohn-Sham) orbitals :
where the unitary matrix is chosen such that the Wannier orbitals are localized in real space. The process of finding a suitable Wannier transformation matrix is known as Wannierization. This page guides you through the steps required to perform Wannierization using the approaches available in VASP.
One-shot Wannierization using a singular-value decomposition
The two main Wannierization methods are projections onto local functions using the LOCPROJ tag and the Selected-Columns-of-the-Density-Matrix (SCDM) method using the LSCDM tag. The LOCPROJ approach offers fine-grained control over the Wannierization process but is also more involved for electronically complex systems. In this case, projection targets have to be chosen and placed manually using the LOCPROJ tag. In contrast, the SCDM approach offers very little control and instead generates Wannier orbitals automatically from a small set of input parameters[1]. This is convenient for systems where the electronic character of the band structure is complicated or unknown.
Both approaches produce as output a matrix . In the case of the LOCPROJ tag, this is the projection matrix between the Bloch orbitals and the local functions, :
The operator is the overlap operator in the projector-augmented-wave method. In the case of the SCDM method, the matrix is the result of an iterative process that extracts local functions from the information contained in the electronic one-particle density matrix.
In general, is not going to be a unitary matrix. It could, in principle, be used to transform the Bloch orbitals into a set of non-orthogonal Wannier orbitals. However, for many applications, it is desirable to have orthonormal Wannier orbitals, such as for Wannier interpolation. Therefore, needs first to be orthonormalized.
In VASP, we employ a one-shot orthonormalization procedure that uses the singular-value decomposition (SVD) of :
which is then used to construct the unitary matrix :
In contrast to iterative methods (e.g., Gram-Schmidt orthogonalization), the SVD orthogonalization operates simultaneously on all local functions. This ensures that the symmetry properties of the local functions encoded in are preserved during the orthonormalization procedure.
LOCPROJ method
To generate Wannier orbitals using local projections, it is sufficient to specify the LOCPROJ tag with suitable projection targets. VASP will then apply the one-shot orthonormalization internally to obtain the Wannier transformation matrix . The number of Wannier orbitals is the same as the total number of local functions.
Tip: You can write the Wannier transformation matrix to disk by setting LWRITE_WANPROJ = true.
|
This information can then be used to perform Wannier interpolation of the electronic band structure (for example, using the KPOINTS_WAN file). It can also be passed to Wannier90 (more on that later).
To find a good representation of the electronic band structure in terms of Wannier orbitals, it is important to choose suitable projection targets. In general, this can be a difficult task as some bands hybridize and disperse, changing electronic character as a function of the Bloch vector . It is thus expedient to understand the relevant electronic bands before attempting a Wannierization using LOCPROJ.
To gain insight into the electronic character of certain bands, you can use the LORBIT tag.
This decomposes the bands into local contributions either in terms of spherical harmonics (LORBIT < 10) or in terms of PAW projector functions (LORBIT ≥ 10).
The relevant information is written to the PROCAR file and can be used to determine suitable projection targets for LOCPROJ.
Example - diamond
Let us examine a small example to highlight the procedure of determining projection targets.
Here, we aim to Wannierize the four highest-lying valence bands of diamond.
This is a group of bands that is energetically isolated (they are surrounded by band gaps).
Since there is no mixing with any other states, the Wannierization process of these four bands is relatively simple.
With the standard C POTCAR distributed with VASP, we can conveniently set NBANDS = 4 to only consider those states.
First, let us run a calculation with LORBIT = 1 and RWIGS = 1.1.
This decomposes the bands into and quantum numbers in terms of spherical harmonics.
We get information on each k-point in the PROCAR file.
Here is the start of the file, which contains information about the Γ-point:
PROCAR lm decomposed
# of k-points: 8 # of bands: 4 # of ions: 2
k-point 1 : 0.00000000 0.00000000 0.00000000 weight = 0.01562500
band 1 # energy -11.73066124 # occ. 2.00000000
ion s py pz px dxy dyz dz2 dxz x2-y2 tot
1 0.508 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.508
2 0.508 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.508
tot 1.016 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.016
band 2 # energy 9.78016466 # occ. 2.00000000
ion s py pz px dxy dyz dz2 dxz x2-y2 tot
1 0.000 0.173 0.173 0.173 0.032 0.032 0.000 0.032 0.000 0.613
2 0.000 0.173 0.173 0.173 0.032 0.032 0.000 0.032 0.000 0.613
tot 0.000 0.346 0.345 0.346 0.063 0.063 0.000 0.063 0.000 1.226
band 3 # energy 9.78126079 # occ. 2.00000000
ion s py pz px dxy dyz dz2 dxz x2-y2 tot
1 0.000 0.305 0.011 0.202 0.002 0.037 0.000 0.056 0.000 0.613
2 0.000 0.305 0.011 0.202 0.002 0.037 0.000 0.056 0.000 0.613
tot 0.000 0.610 0.023 0.404 0.004 0.074 0.000 0.112 0.000 1.226
band 4 # energy 9.78126093 # occ. 2.00000000
ion s py pz px dxy dyz dz2 dxz x2-y2 tot
1 0.000 0.041 0.334 0.143 0.061 0.026 0.000 0.007 0.000 0.613
2 0.000 0.041 0.334 0.143 0.061 0.026 0.000 0.007 0.000 0.613
tot 0.000 0.081 0.668 0.287 0.122 0.052 0.000 0.015 0.000 1.226
From this, we learn that the four valence bands are predominantly s-like and p-like (make sure that this is true also at the other k-points). This was to be expected since carbon forms hybridized sp-3 bonds in diamond.
With this information, we can now specify projection targets. We seek to map the four bands in the simulation to four Wannier orbitals, so we choose to setup four sp-3 hybrids on one atom. The minimal INCAR file used in this example looks like this:
ISMEAR = 0 ! use Gaussian smearing for insulator SIGMA = 0.01 ! use small smearing NBANDS = 4 ! use only 4 bands LOCPROJ = 1 : sp3 : Hy 1 4. ! ... to map onto 4 sp-3 functions
The last part of the LOCPROJ setting (Hy 1 4.) specifies that we want Hyrdogen-like atomic orbitals (spherical harmonics) with main quantum number and a diffusivity of . The diffusivity influences the spread of the local function. A higher value generally results in a higher degree of localization. This is beneficial for Wannier interpolation and yields Wannier orbitals of higher quality in that regard.
Tip: You may also choose to use the PAW information to specify local orbitals with LOCPROJ. In this case, you should use LORBIT = 11 to extract the relevant information from the basis.
|
For this example calculation, we use a relatively course Γ-centered regular mesh of 4x4x4 k-points.
To gauge the quality of the generated Wannier orbitals, we can plot the electronic band structure using Wannier interpolation and compare it against the ab-initio data. As of VASP 6.3.0, this can conveniently be done all in one run by providing the KPOINTS_OPT and the KPOINTS_WAN file. These files are automatically read from disk and provide a way to calculate the electronic eigenvalues at specific k-points.
- KPOINTS_OPT: Charge density is kept fixed and the Hamiltonian is diagonalized at each provided k-point.
- KPOINTS_WAN: Hamiltonian is constructed, interpolated and diagonalized using the Wannier orbitals.
Importantly, these k-points can be different from those specified in the KPOINTS file.
Here, we specify a k-point path through the first Brillouin zone using the line mode for both files. The results can then be read from the vaspout.h5 at the following locations:
results/electron_eigenvalues_kpoints_opt/ results/electron_eigenvalues_kpoints_wan/
The results can be seen in the following band-structure plot:
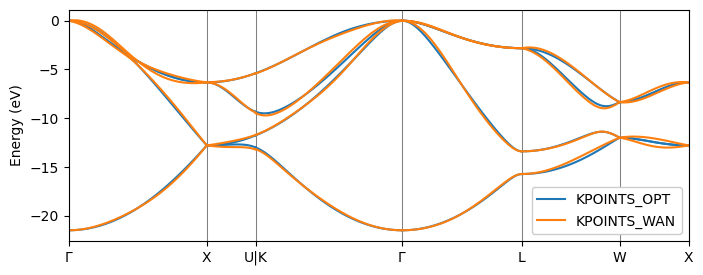
The agreement between both methods is already very good. The remaining differences can be systematically decreased by increasing the k-point density in the initial KPOINTS file or by choosing a more suitable local basis.
SCDM method
In contrast to the LOCPROJ method, the SCDM method does not rely on the specification of a local basis.
To activate the SCDM method, set LSCDM = true.
This will use the information contained in the electronic one-particle density matrix to construct localized functions from the original Bloch (Kohn-Sham) orbitals.
These localized functions are then orthonormalized using the one-shot SVD approach to obtain orthonormal Wannier orbitals.
The number of Wannier orbitals obtained is controlled via the NUM_WANN tag.
Mind: You must ensure that NUM_WANN ≤ NBANDS in order to have enough information to construct the Wannier orbitals.
|
Example - diamond
Let us repeat the example calculation shown earlier to obtain Wannier orbitals in diamond using the SCDM method.
Once again, we choose NBANDS = 4 and we set NUM_WANN = 4 as well.
The minimal INCAR file for this example looks like this:
ISMEAR = 0 ! use Gaussian smearing for insulator SIGMA = 0.01 ! use small smearing NBANDS = 4 ! use only 4 bands NUM_WANN = 4 ! ... to map onto 4 Wannier orbitals LSCDM = true ! ... using the SCDM method
For this example calculation, we use the same course Γ-centered regular mesh of 4x4x4 k-points as before. We also specify the same k-point path for KPOINTS_OPT and KPOINTS_WAN to perform band-structure calculations. The results can be seen in the following band-structure plot:
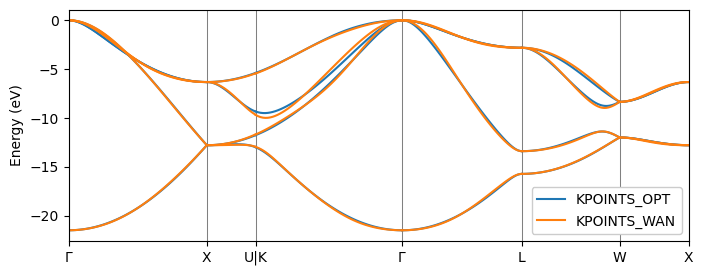
Also in this case, the agreement between both methods is very good.
Comparison with LOCPROJ
The diamond example shows that a Wannierization of good quality can be achieved with both the LOCPROJ as well as the SCDM approach. However, the bands considered in that example are fully isolated from the rest of the band structure and their electronic character is well known.
In general, finding suitable projection targets can be a difficult and arduous task. This is where the more automatic SCDM method has a clear advantage over the LOCPROJ approach. The SCDM method extracts the electronic character of the bands directly from the density matrix. On the other hand, the LOCPROJ approach requires the user to have a good understanding of the band structure of the material.
However, specifying local functions via LOCPROJ also has advantages over the SCDM method. First, there is very little control over the orbitals that the SCDM method generates because the number of calculational parameters is so small. This can be undesirable if the location, shape or symmetry of the Wannier orbital is important. With LOCPROJ, you can choose the kind of orbital much more freely, for example, to study chemical bonding. Second, SCDM orbitals do not generally obey the same symmetries as the crystal or as molecular bonds. This is because the SCDM procedure employs an iterative scheme for choosing "optimal" localized functions one after the other (this is based on a rank-revealing QR decomposition). As such, orbitals that should be symmetrically equivalent such as the hybridized sp-3 orbitals in the case of diamond end up being slightly different from each other. Consequently, the Wannier interpolation of the electronic band structure using SCDM orbitals will not be able to perfectly reproduce degeneracies since the underlying symmetries are broken. Usually, this difference is comparatively small but it is something to keep in mind.
Disentanglement
When NBANDS > NUM_WANN or when the bands are not energetically isolated, Wannierization becomes more involved.
The difficulty lies in determining which electronic states to select when transforming the initial Bloch orbitals to the Wannier orbitals.
This process is known as disentanglement.
When using the LOCPROJ or SCDM methods, disentanglement can be achieved by applying a smooth cutoff or weight function to the electronic states during the Wannierization process.
Loosely speaking, electronic states with a larger weight will be fitted more accurately.
In VASP, we currently support three types of cutoff functions that can be selected via CUTOFF_TYPE, erfc, gaussian and fermi.
The tags CUTOFF_MU and CUTOFF_SIGMA control the position, , and width, , of these cutoff functions, respectively.
The complementary error function and Fermi function are particularly useful in scenarios where the band structure does not have a gap above the relevant energies, such as in metals. The Gaussian function is useful for extracting a Wannier representation from a group of bands that is not surrounded by any gaps, below or above.
Example - SCDM Wannierization of LiF
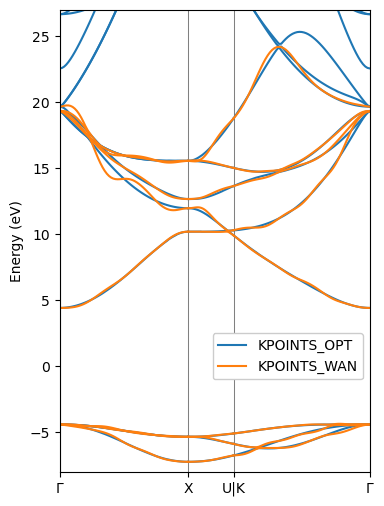
LiF is an insulator with a wide band gap. The Wannierization of the valence states in isolation is as simple as shown earlier. However, the lowest-lying conduction states are relatively dispersive and hybridize with higher-lying states. This renders the Wannierization of these conduction bands difficult without disentanglement.
To obtain the lowest lying conduction bands of LiF, we choose the erfc cutoff function with an appropriate and .
By default, VASP chooses reasonable default values for these parameters.
However, in order to get a good Wannier fit of the band structure, both and should be chosen carefully by the user through trial and error.
As a rule of thumb, the smooth edge of the complementary error function should be positioned such that states below it are to be fitted more accurately.
For this example, we have chosen and , which places the edge of the cutoff function amidst the lowest-lying conduction bands with a relatively sharp edge.
The minimal INCAR file for this example is provided below:
ISMEAR = 0 ! use Gaussian smearing for insulator SIGMA = 0.01 ! use small smearing NBANDS = 16 ! use 16 bands, including unoccupied states NUM_WANN = 9 ! ... to map to 9 Wannier orbitals LSCDM = true ! ... using the SCDM method CUTOFF_TYPE = erfc ! choose erfc cutoff function CUTOFF_MU = 10 ! ... and place it at 10 eV CUTOFF_SIGMA = 0.1 ! ... with a width of 0.1 eV
The initial k-point mesh is chosen to be 8x8x8 Γ-centered.
The Wannier-interpolated band structure compares favorably against the ab-initio data below and starts to diverge from it more and more above . This is a general trend with these kinds of calculations and is an unavoidable side effect of the disentanglement procedure. The alternative would be a much higher and sharper cutoff that requires more Wannier states to be constructed. This is however not generally advisable as it can negatively affect the quality of the Wannierization.
| Tip: A hard cutoff can be achieved by specifying a tiny CUTOFF_SIGMA. |
| Mind: The quality of the Wannierization can depend strongly on the choice of CUTOFF_MU and CUTOFF_SIGMA. It will often take some trial and error to find reasonable parameters. |
Wannier90
Wannier orbitals obtained inside VASP via the LOCPROJ or SCDM methods can be passed to Wannier90 for further processing. Wannier90 employs an iterative algorithm that generates so-called maximally-localized Wannier functions (MLWF). MLWFs are usually superior in terms of quality for band structure calculations. However, even though they are generated from an iterative procedure, Wannier90 still relies on good first guesses for the localized functions. This is where the SCDM method can provide a suitable set of initial functions for the MLWF procedure. In the case of the LOCPROJ tag, the projection matrix is passed directly to Wannier90 where the Wannier transformation is constructed. VASP handles the communication of the projection targets and matrix dimensions automatically.
To generate MLWFs from VASP orbitals, you can add the following lines to your INCAR file:
LWANNIER90 = true # or lwannier90_run = true WANNIER90_WIN = " dis_num_iter = 100 num_iter = 100 "
where dis_num_iter specifies the number of iteration during Wannier90's disentanglement procedure and num_iter the number of iteration during the MLWF procedure.
| Important: Make sure that VASP is compiled with the VASP2WANNIER90 precompiler option. |
Important: When using the SCDM method together with Wannier90, it is recommended to set dis_num_iter = 0 via WANNIER90_WIN or in the Wannier90 input file.
|
LWANNIER90 activates the interface between VASP and Wannier90 and writes a wannier90.win input file that can then be read by Wannier90. In addition to the basic input parameters, VASP also writes the overlap matrices and to the corresponding files, wannier90.mmn and wannier90.amn. contains the overlaps between all pairs of Bloch orbitals. Meanwhile, contains the overlaps between the Bloch orbitals and the projection targets (in this case, the SCDM orbitals obtained from VASP).
Tip: The wannier90.mmn and wannier90.amn files can be explicitly written via LWRITE_MMN_AMN = true. This is switched on by default when LWANNIER90 = true. It is unnecessary to write these files when LWANNIER90_RUN = true as they are directly passed to Wannier90.
|
Run VASP with the above INCAR tags to generate Wannier orbitals via SCDM or LOCPROJ and to generate the required Wannier90 input files.
Afterwards, run Wannier90 to generate MLWFs (all of this can be done in one run when setting LWANNIER90_RUN = true).
At this point, you can use the functionality available in Wannier90 to plot the band structure, the orbitals, etc.
When plotting orbitals using Wannier90, in addition to LWRITE_MMN_AMN = true, it may also be necessary to set LWRITE_UNK = true.
This writes the cell-periodic part of the Bloch orbitals to disk.
Related tags and articles
LSCDM, LOCPROJ, CUTOFF_TYPE, CUTOFF_MU, CUTOFF_SIGMA
