Constrained–random-phase–approximation formalism: Difference between revisions
No edit summary |
|||
| (39 intermediate revisions by 2 users not shown) | |||
| Line 15: | Line 15: | ||
=== Wannier basis and target space === | === Wannier basis and target space === | ||
To use model Hamiltonians successfully a localized basis set is chosen. | To use model Hamiltonians successfully a localized basis set is chosen. | ||
In most applications this basis set consists of [[ | In most applications this basis set consists of [[Wannier_functions|Wannier states]] that are connected with the Bloch functions <math>\psi_{n\bf k}^\sigma ({\bf r}) = e^{i{\bf k r}} u_{n\bf k}({r})</math> of band <math>n</math> at k-point <math>k</math> with spin <math>\sigma</math> via | ||
::<math> | ::<math> | ||
| w_{i\bf R}^\sigma \rangle = \frac{1}{N_k}\sum_{n\bf k} e^{-i {\bf k R}} T_{i n}^{\sigma({\bf k})} | \psi_{n\bf k}^\sigma \rangle | | w_{i\bf R}^\sigma \rangle = \frac{1}{N_k}\sum_{n\bf k} e^{-i {\bf k R}} T_{i n}^{\sigma({\bf k})} | \psi_{n\bf k}^\sigma \rangle | ||
| Line 24: | Line 24: | ||
</math> | </math> | ||
{{NB|mind|Here, T instead of the widely used U notation for the transformation matrix is used to avoid confusion with the Hubbard parameter.}} | {{NB|mind|Here, T instead of the widely used U notation for the transformation matrix is used to avoid confusion with the Hubbard parameter.}} | ||
In practice one builds a model Hamiltonian only for a small subset of Bloch functions. These '''target states''' are typically centered around the chemical potential (or Fermi energy) and are strongly localized around ions. The model Hamiltonian can be solved successfully | In practice, one builds a model Hamiltonian only for a small subset of Bloch functions. These '''target states''' are typically centered around the chemical potential (or Fermi energy) and are strongly localized around ions. The model Hamiltonian can be solved successfully only if the target states are well represented by the Wannier basis. | ||
As a measure of the Wannier representation one usually compares the original band structure with the Wannier interpolated one. | As a measure of the Wannier representation, one usually compares the original band structure with the Wannier interpolated one. | ||
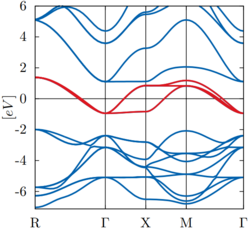
In the following example (SrVO3) the target space consists of three Bloch bands (red bands) that may be represented well by three Wannier states: | In the following example (SrVO3), the target space consists of three Bloch bands (red bands) that may be represented well by three Wannier states: | ||
[[File:SrVO3_t2g_bands.png|250px]] | [[File:SrVO3_t2g_bands.png|250px]] | ||
The complete target space is spanned by a certain number of Bloch bands. These bands can be selected with the {{TAG|NCRPA_BANDS}} tag. | |||
More often, however, one has delocalized states that mix with the target space of the model. | More often, however, one has delocalized states that mix with the target space of the model. | ||
Without including these | Without including these additional states in the Wannier basis, a good representation of the band structure is not possible. | ||
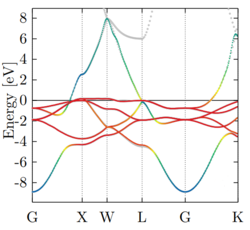
Below is an example (face-centered-cubic Ni), where the delocalized s-band (blue) crosses the five target d-states (red): | Below is an example (face-centered-cubic Ni), where the delocalized s-band (blue) crosses the five target d-states (red): | ||
[[File:Ni_d_s_bands.png|250px]] | [[File:Ni_d_s_bands.png|250px]] | ||
This system requires at least six Wannier states to represent the electronic structure of five target states well. | This system requires at least six Wannier states to represent the electronic structure of five target states well. | ||
The selection of target states in the Wannier basis is done with the {{TAG|NTARGET_STATES}}. | |||
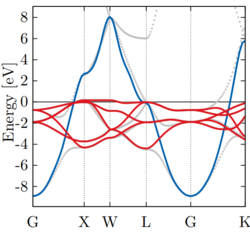
If a modification of the band structure is acceptable within an energy window, these five target states might be '''disentangled''' from the remaining ones and one arrives at following picture: | If a modification of the band structure is acceptable within an energy window, these five target states might be '''disentangled''' from the remaining ones, and one arrives at the following picture: | ||
[[File:Ni_d_bands_decoupled.png|250px]] | [[File:Ni_d_bands_decoupled.png|250px]] | ||
| Line 47: | Line 48: | ||
Here the original Bloch bands (gray lines) are projected to five non-crossing Wannier states. | Here the original Bloch bands (gray lines) are projected to five non-crossing Wannier states. | ||
In the following <math>\cal T</math> denotes | In the following <math>\cal T</math> denotes the '''target space''', that is, the states described by the model Hamiltonian. | ||
=== Parameter definitions === | === Parameter definitions === | ||
| Line 87: | Line 88: | ||
In analogy to the [[GW approximation of Hedin's equations#W_reci|screened Coulomb kernel in GW]], the effective coulomb kernel is calculated as | In analogy to the [[GW approximation of Hedin's equations#W_reci|screened Coulomb kernel in GW]], the effective coulomb kernel is calculated as | ||
::<math> | ::<math> | ||
U^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},\omega)=\left[\delta_{{\bf G}{\bf G}'}-(\chi^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},\omega) - \tilde\chi^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},\omega) ) \cdot V_{{\bf G}{\bf G}'}({\bf q})\right]^{-1}V_{{\bf G}{\bf G}'}({\bf q}) | U^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},i\omega)=\left[\delta_{{\bf G}{\bf G}'}-(\chi^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},i\omega) - \tilde\chi^{\sigma\sigma'}_{{\bf G}{\bf G}'}({\bf q},i\omega) ) \cdot V_{{\bf G}{\bf G}'}({\bf q})\right]^{-1}V_{{\bf G}{\bf G}'}({\bf q}) | ||
</math> | </math> | ||
In contrast to the GW method, however, the polarizability contains all RPA screening effects | In contrast to the GW method, however, the polarizability contains all RPA screening effects except those from the target space. These effects are described by <math>\tilde \chi</math>. In the following four methods are presented for the calculation of <math>\tilde \chi</math>. | ||
These effects are described by <math>\tilde \chi</math> | {{NB|mind|All methods below reduce to the '''band method''' if the target space forms an isolated set of bands.}} | ||
{{NB|tip|Select cRPA methods with {{TAG|ALGO}} {{=}} CRPA.}} | |||
</math> | |||
=== Band method === | |||
The simplest way to define the target polarizability is to use the expression of Adler and Wiser{{cite|adler:1962}}{{cite|wiser:1963}}{{cite|aryasetiawan:prb70}} | |||
::<math>\tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)= | ::<math>\tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)= | ||
\frac 1{N_k}\sum_{ | \frac 1{N_k}\sum_{\bf k}\sum_{nn'\in{\cal T}} | ||
\sum_{ | |||
\frac{ | \frac{ | ||
f_{n\bf k}-f_{n'\bf k-q} | f_{n\bf k}-f_{n'\bf k-q} | ||
| Line 138: | Line 104: | ||
\epsilon_{n{\bf k}} - \epsilon_{n'\bf k-q} - i \omega | \epsilon_{n{\bf k}} - \epsilon_{n'\bf k-q} - i \omega | ||
} | } | ||
\langle | \langle | ||
u_{ | u_{n {\bf k }}^{\sigma } | ||
|e^{-i \bf (G+q) r}| | |e^{-i \bf (G+q) r}| | ||
u_{ | u_{n'{\bf k-q}}^{ \sigma' } | ||
\rangle | \rangle | ||
\langle | \langle | ||
u_{ | u_{n' {\bf k-q}}^{\sigma' } | ||
|e^{-i \bf (G'-q)r'} | | |e^{-i \bf (G'-q)r'} | | ||
u_{ | u_{n{\bf k }}^{ \sigma } | ||
\rangle | \rangle | ||
</math> | </math> | ||
This approach is most accurate for an isolated target space <math>\cal T</math> as depicted in the first example above. | |||
{{NB|mind|Target bands can be selected with {{TAG|NCRPA_BANDS}}.}} | |||
{{NB|mind| | {{NB|warning|This method is not suited for systems with entangled target states.}} | ||
=== Disentanglement method === | === Disentanglement method === | ||
Miyake, Aryasetiawan and Imada{{cite|miyake:prb:80}} propose to disentangle the target space from the full space | Miyake, Aryasetiawan, and Imada{{cite|miyake:prb:80}} propose to disentangle the target space from the full space by diagonalizing the Hamiltonian in both spaces independently. | ||
This yields a band disentangled band structures similar to the one shown in the third example above. | This yields a band disentangled band structures similar to the one shown in the third example above. | ||
The corresponding target polarizability reduces to a constrained Alder and Wiser expression{{cite|adler:1962}}{{cite|wiser:1963}} | The corresponding target polarizability reduces to a constrained Alder and Wiser expression{{cite|adler:1962}}{{cite|wiser:1963}} | ||
| Line 175: | Line 131: | ||
} | } | ||
\langle | \langle | ||
\tilde u_{n {\bf k }}^{ | \tilde u_{n {\bf k }}^{\sigma } | ||
|e^{-i \bf (G+q) r}| | |e^{-i \bf (G+q) r}| | ||
\tilde u_{n'{\bf k-q}}^{ \sigma' } | \tilde u_{n'{\bf k-q}}^{ \sigma' } | ||
\rangle | \rangle | ||
\langle | \langle | ||
\tilde u_{n' {\bf k-q}}^{ | \tilde u_{n' {\bf k-q}}^{\sigma' } | ||
|e^{-i \bf (G'-q)r'} | | |e^{-i \bf (G'-q)r'} | | ||
\tilde u_{n{\bf k }}^{ \sigma } | \tilde u_{n{\bf k }}^{ \sigma } | ||
| Line 187: | Line 143: | ||
where <math>\tilde \epsilon_{n\bf k}^\sigma</math> is the disentangled band structure. | where <math>\tilde \epsilon_{n\bf k}^\sigma</math> is the disentangled band structure. | ||
The resulting Hubbard-Kanamori interactions depend on the chosen energy window of the Wannier functions. | The resulting Hubbard-Kanamori interactions depend on the chosen energy window of the Wannier functions. | ||
{{NB|mind|Typically, this method yields the largest Hubbard-Kanamori interactions.}} | {{NB|mind|Typically, this method yields the largest Hubbard-Kanamori interactions and is selected with {{TAG|LDISENTANGLED}} tag.}} | ||
=== Weighted | === Weighted method === | ||
Sasioglu, Friedrich and Blügel propose an alternative approach | Sasioglu, Friedrich and Blügel propose an alternative approach.{{cite|sasioglu:prb:83}} | ||
They calculate the screening effects within the target space as follows: | |||
::<math>\tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)\approx | ::<math>\tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)\approx | ||
\frac 1{N_k}\sum_{nn'{\bf k}} | \frac 1{N_k}\sum_{nn'{\bf k}} | ||
| Line 201: | Line 158: | ||
p_{n'\bf k-p }^{\sigma'} | p_{n'\bf k-p }^{\sigma'} | ||
\langle | \langle | ||
u_{n {\bf k }}^{ | u_{n {\bf k }}^{\sigma } | ||
|e^{-i \bf (G+q) r}| | |e^{-i \bf (G+q) r}| | ||
u_{n'{\bf k-q}}^{ \sigma' } | u_{n'{\bf k-q}}^{ \sigma' } | ||
\rangle | \rangle | ||
\langle | \langle | ||
u_{n' {\bf k-q}}^{ | u_{n' {\bf k-q}}^{\sigma' } | ||
|e^{-i \bf (G'-q)r'} | | |e^{-i \bf (G'-q)r'} | | ||
u_{n'{\bf k }}^{ \sigma } | u_{n'{\bf k }}^{ \sigma } | ||
| Line 215: | Line 172: | ||
</math> | </math> | ||
measure the probability for <math>|\psi_{n\bf k}^\sigma\rangle</math> being in the target space. | measure the probability for <math>|\psi_{n\bf k}^\sigma\rangle</math> being in the target space. | ||
This method does not alter the band structure, however, neglects screening effects within the target space. | This method does not alter the band structure, however, neglects screening effects within the target space as shown in next section. | ||
{{NB|mind| | Typically, the weighted cRPA method yields the smallest Hubbard-Kanamori interactions. | ||
{{NB|mind|This method is selected with the {{TAG|LWEIGHTED}} tag.}} | |||
=== Projector method === | |||
A consistent expression for the target polarizability gives rise to the projector-cRPA method. | |||
The main goal is to subdivide the target from the full Fock space in a Wannier basis. | |||
To this end, we work with the target projectors | |||
::<math> | |||
P_{mn}^{\sigma({\bf k})} = \sum_{i\in \cal T} T_{i m}^{*\sigma({\bf k})} T_{i n}^{\sigma({\bf k})} | |||
</math> | |||
that filter out target space contributions to each Bloch state. Using these projectors, | |||
the target polarizability for the projector method reads{{cite|kaltak:thesis2015}} | |||
::<math>\tilde \chi^\sigma_{{\bf G,G}'}({\bf q},i\omega)= | |||
\frac 1{N_k}\sum_{nn'{\bf k}} | |||
\frac{ | |||
f_{n\bf k}-f_{n'\bf k-q} | |||
}{ | |||
\epsilon_{n{\bf k}} - \epsilon_{n'\bf k-q} - i \omega | |||
} | |||
\times | |||
\sum_{m_1m_2' } | |||
P_{m_1 n }^{*\sigma ({\bf k })} | |||
\langle | |||
u_{m_1 {\bf k }}^{\sigma } | |||
|e^{-i \bf (G+q) r}| | |||
u_{m_2'{\bf k-q}}^{ \sigma' } | |||
\rangle | |||
P_{m_2' n'}^{ \sigma' ({\bf k-q})} | |||
\times | |||
\sum_{m_1'm_2 } | |||
P_{m_2 n'}^{*\sigma' ({\bf k-q})} | |||
\langle | |||
u_{m_2 {\bf k-q}}^{\sigma' } | |||
|e^{-i \bf (G'-q)r'} | | |||
u_{m_1'{\bf k }}^{ \sigma } | |||
\rangle | |||
P_{m_1' n }^{ \sigma ({\bf k })} | |||
</math> | |||
The projector method usually results in larger (smaller) Hubbard-Kanamori interactions than the weighted (disentanglement) method. | |||
{{NB|mind|The projector method is the default cRPA method.}} | |||
== Caveats == | |||
The cRPA method is usually applied to systems with a zero-band gap (metallic system) and, thus, suffers from slow k-point convergence. | |||
Most reliably, the usage of k-p perturbation theory should be avoided. That is, {{TAG|LOPTICS}}=.FALSE. should be set in the preceding DFT step and/or the {{FILE|WAVEDER}} should be deleted before the cRPA step. | |||
{{NB|tip|If {{TAG|NCRPA_BANDS}} is set in the INCAR and includes all partially occupied bands, one can use WAVEDER in cRPA calculations to accelerate k-point convergence.}} | |||
== Related tags and articles== | == Related tags and articles== | ||
{{TAG|ALGO}}, | {{TAG|ALGO}}, | ||
{{TAG|NTARGET_STATES}}, | {{TAG|NTARGET_STATES}}, | ||
{{TAG|NCRPA_BANDS}} | {{TAG|NCRPA_BANDS}}, | ||
{{TAG| | {{TAG|LDISENTANGLED}}, | ||
{{TAG|LWEIGHTED}} | {{TAG|LWEIGHTED}}, | ||
{{TAG|NUM_WANN}} | {{TAG|NUM_WANN}}, | ||
{{TAG|WANNIER90_WIN}} | {{TAG|WANNIER90_WIN}}, | ||
{{TAG|ENCUTGW}} | {{TAG|ENCUTGW}}, | ||
{{TAG|VCUTOFF}} | {{TAG|VCUTOFF}} | ||
| Line 232: | Line 233: | ||
<references/> | <references/> | ||
---- | ---- | ||
[[Category:Theory]][[Category:Many- | [[Category:Theory]][[Category:Many-body perturbation theory]][[Category:Constrained-random-phase approximation]][[Category:Wannier functions]] | ||
Latest revision as of 14:38, 20 February 2024
The constrained random-phase approximation (CRPA) is a method that allows to calculate the effective interaction parameter U, J and J' for model Hamiltonians. The main idea is to neglect screening effects of specific target states in the screened Coulomb interaction W of the GW method. The resulting partially screened Coulomb interaction is usually evaluated in a localized basis that spans the target space and is described by the model Hamiltonian. Usually, the target space is low-dimensional (up to 5 states) and therefore allows for the application of a higher level theory, such as dynamical mean field theory (DMFT).
Model Hamiltonians
A model Hamiltonian describes a small subset of electrons around the chemical potential and has, in second quantization, following form
Here, are site and spin indices, respectively and the symbol indicates summation over nearest neighbors. The hopping matrix elements describe the hopping of electrons (of same spin) between site and , while the effective Coulomb matrix elements describe the interaction of electrons between sites.
Wannier basis and target space
To use model Hamiltonians successfully a localized basis set is chosen. In most applications this basis set consists of Wannier states that are connected with the Bloch functions of band at k-point with spin via
Usually, the basis set is localized such that the interaction between periodic images can be neglected. This allows to work with the Wannier functions in the unit cell at :
| Mind: Here, T instead of the widely used U notation for the transformation matrix is used to avoid confusion with the Hubbard parameter. |
In practice, one builds a model Hamiltonian only for a small subset of Bloch functions. These target states are typically centered around the chemical potential (or Fermi energy) and are strongly localized around ions. The model Hamiltonian can be solved successfully only if the target states are well represented by the Wannier basis. As a measure of the Wannier representation, one usually compares the original band structure with the Wannier interpolated one.
In the following example (SrVO3), the target space consists of three Bloch bands (red bands) that may be represented well by three Wannier states:
The complete target space is spanned by a certain number of Bloch bands. These bands can be selected with the NCRPA_BANDS tag.
More often, however, one has delocalized states that mix with the target space of the model. Without including these additional states in the Wannier basis, a good representation of the band structure is not possible. Below is an example (face-centered-cubic Ni), where the delocalized s-band (blue) crosses the five target d-states (red):
This system requires at least six Wannier states to represent the electronic structure of five target states well. The selection of target states in the Wannier basis is done with the NTARGET_STATES.
If a modification of the band structure is acceptable within an energy window, these five target states might be disentangled from the remaining ones, and one arrives at the following picture:
Here the original Bloch bands (gray lines) are projected to five non-crossing Wannier states.
In the following denotes the target space, that is, the states described by the model Hamiltonian.
Parameter definitions
| Mind: The calculation of the hopping matrix depends on the theory that is used to solve the effective model. |
For instance, in DFT+DMFT (often termed LDA+DMFT) one calculates the hopping matrix from Kohn-Sham energies, while in GW+DMFT GW quasi-particle energies are used. If denotes these one-electron energies and is the corresponding Fermi energy, the hopping matrix elements are calculated with following formula
Similarly, Coulomb matrix elements are evaluated from the Bloch representation of the effective Coulomb kernel via
| Mind: The effective Coulomb kernel is frequency dependent and thus the effective interaction in the model as well. |
In most applications, however, one considers the static limit .
In practice one often, simplifies the model Hamiltonian further and works with the Hubbard-Kanamori parameters:[1]
Here specifies the number of Wannier functions in the target space .
Effective Coulomb kernel in constrained random-phase approximation
In analogy to the screened Coulomb kernel in GW, the effective coulomb kernel is calculated as
In contrast to the GW method, however, the polarizability contains all RPA screening effects except those from the target space. These effects are described by . In the following four methods are presented for the calculation of .
| Mind: All methods below reduce to the band method if the target space forms an isolated set of bands. |
| Tip: Select cRPA methods with ALGO = CRPA. |
Band method
The simplest way to define the target polarizability is to use the expression of Adler and Wiser[2][3][4]
This approach is most accurate for an isolated target space as depicted in the first example above.
| Mind: Target bands can be selected with NCRPA_BANDS. |
| Warning: This method is not suited for systems with entangled target states. |
Disentanglement method
Miyake, Aryasetiawan, and Imada[5] propose to disentangle the target space from the full space by diagonalizing the Hamiltonian in both spaces independently. This yields a band disentangled band structures similar to the one shown in the third example above. The corresponding target polarizability reduces to a constrained Alder and Wiser expression[2][3]
- ,
where is the disentangled band structure. The resulting Hubbard-Kanamori interactions depend on the chosen energy window of the Wannier functions.
| Mind: Typically, this method yields the largest Hubbard-Kanamori interactions and is selected with LDISENTANGLED tag. |
Weighted method
Sasioglu, Friedrich and Blügel propose an alternative approach.[6] They calculate the screening effects within the target space as follows:
Here the weighting factors
measure the probability for being in the target space. This method does not alter the band structure, however, neglects screening effects within the target space as shown in next section. Typically, the weighted cRPA method yields the smallest Hubbard-Kanamori interactions.
| Mind: This method is selected with the LWEIGHTED tag. |
Projector method
A consistent expression for the target polarizability gives rise to the projector-cRPA method. The main goal is to subdivide the target from the full Fock space in a Wannier basis. To this end, we work with the target projectors
that filter out target space contributions to each Bloch state. Using these projectors, the target polarizability for the projector method reads[7]
The projector method usually results in larger (smaller) Hubbard-Kanamori interactions than the weighted (disentanglement) method.
| Mind: The projector method is the default cRPA method. |
Caveats
The cRPA method is usually applied to systems with a zero-band gap (metallic system) and, thus, suffers from slow k-point convergence. Most reliably, the usage of k-p perturbation theory should be avoided. That is, LOPTICS=.FALSE. should be set in the preceding DFT step and/or the WAVEDER should be deleted before the cRPA step.
| Tip: If NCRPA_BANDS is set in the INCAR and includes all partially occupied bands, one can use WAVEDER in cRPA calculations to accelerate k-point convergence. |
Related tags and articles
ALGO, NTARGET_STATES, NCRPA_BANDS, LDISENTANGLED, LWEIGHTED, NUM_WANN, WANNIER90_WIN, ENCUTGW, VCUTOFF
References
- ↑ L. Vaugier, H. Jiang, and S. Biermann, Phys. Rev. B 86, 165105 (2012).
- ↑ a b S. L. Adler, Phys. Rev. 126, 413 (1962)
- ↑ a b N. Wiser, Phys. Rev. 129, 62 (1963)
- ↑ F. Aryasetiawan, M. Imada, A. Georges, G. Kotliar, S. Biermann, and A. I. Lichtenstein, Phys. Rev. B 70, 195104 (2004).
- ↑ T. Miyake, F. Aryasetiawan, and M. Imada, Phys. Rev. B 80, 155134 (2009).
- ↑ E. Sasioglu, C. Friedrich, and S. Blügel, Phys. Rev. B 83, 121101 (2011).
- ↑ M. Kaltak, Thesis: Merging GW with DMFT (2015).